Vamos
a dedicar esta entrada a realizar una introducción a las principales
características del sistema diédrico de representación. Para ello,
nos resultará de utilidad identificar algunas diferencias entre su
uso con línea de tierra (LT) y sin línea de tierra (método directo
o sistema libre de representación).
Como
sabemos, si queremos representar elementos del espacio tridimensional
sobre un plano, necesitamos de sistemas que nos permitan trasladarlos
al papel. Para ello, los sistemas se valen de la representación
de las proyecciones de dichos elementos sobre un plano
imaginario. Estas proyecciones contienen la información
que necesitamos para interpretar los elementos sin errores (con
cualquier objetivo: didáctico, de fabricación industrial, para
resolver problemas, etc).
En
el siguiente vídeo podemos ver una breve introducción a los
sistemas de representación:
En
el vídeo (además de cuestiones que nos resultará de utilidad más adelante), hemos podido observar los tres tipos de proyección de los
sistemas de representación: Cónica, Cilíndrica Ortogonal y
Cilíndrica Oblicua.
¡Pero
vamos al asunto de esta entrada! El sistema diédrico.
La
primera característica del sistema diédrico, es la condición de
perpendicularidad que siempre van a cumplir sus dos planos de
proyección, que son:
Plano
horizontal de proyección (PH)
Plano
vertical de proyección (PV)
Esta
perpendicularidad se va a cumplir SIEMPRE en el sistema diédrico,
tanto en el que utiliza línea de tierra (LT) como en el método
directo. Sin embargo, hay unas diferencias básicas:
- En el sistema diédrico con LT, el plano de proyección horizontal interseca con el plano de proyección vertical (figura 1), obteniendo como resultados de la intersección: la línea de tierra y los cuatro cuadrantes o diedros. Al abatir el PH (en sentido horario) sobre el PV, obtendremos estos cuatro cuadrantes o diedros representados en un solo plano. De este plano abatido con la línea de tierra como referencia (figura 2), podemos obtener las posiciones absolutas (sistema de coordenadas absolutas) con respecto a los cuatro diedros o cuadrantes.
- El sistema diédrico directo, utiliza planos de proyección cualesquiera paralelos a un cuadrante o diedro de referencia (primer cuadrante en el caso del Sistema Europeo de Representación Normalizada de Vistas). Es decir, que los planos de proyección no intersecan y por tanto, no se obtiene la línea de tierra. De este método, tampoco se va a obtener la posición absoluta de los elementos con respecto a los cuadrantes, sino que: la posición de los elementos va a ser siempre relativa (sistema de coordenadas relativas) a otros elementos. Por este motivo, en el diédrico directo la planta y el perfil de los objetos se puede situar a cualquier distancia del alzado.
Tanto
si usamos línea de tierra como si no, el sistema diédrico se basa
en la proyección cilíndrica ortogonal, es decir, que los
elementos se proyectan ortogonalmente al plano (figura 4 y figura 5).
Para entender mejor
este concepto, vamos a introducir la representación del elemento más
básico –no por ello con menos posibilidades de análisis–: el
punto, primero con línea de tierra:
Como
hemos visto, la nomenclatura y la posición de las proyecciones del
punto con respecto a la línea de tierra, nos dará la información
que necesitamos para saber en qué cuadrante se encuentra el punto
representado y su posición. También podemos determinar un origen O
sobre la línea de tierra y representar al punto por coordenadas.
Para ello, establecemos el origen O como vértice de un sistema de
ejes ortogonales.
De
este sistema de ejes ortogonales, obtendremos las coordenadas diédricas (pues
los diedros son la referencia), siendo:
x:
la distancia del origen a la línea de referencia del punto
y:
el alejamiento
z:
la cota
Que
como hemos visto serán positivas o negativas según la posición de
los elementos con respecto al origen.
Sin
embargo, a la hora de de representar el punto con el sistema libre,
nos encontraremos con la duda de cómo empezar
sin ninguna referencia establecida. Pues bien, la representación de
un punto A va a ser arbitraria en cuanto a la separación de sus
proyecciones (es decir, la línea de referencia).
Para determinar su posición, aplicaremos un sistema de coordenadas
relativas entre A y B (ver figura 6), siendo:
x:
separación de las líneas de referencias
y:
diferencia de cotas
z:
diferencia de alejamientos
 |
| Figura 6. Coordenadas relativas entre A y B. Imagen de
|
Ambos
sistemas nos permiten representar la situación del punto en el PV y
el PH. La diferencia principal, es que el sistema libre elimina
referentes que no son necesarios (simplifica el proceso) y el estudio
de los elementos resulta mucho más conceptual. Por este motivo,
conviene tener muy claros algunos conceptos básicos para representar
los elementos de una manera correcta (y mucho más ágil).
Entre
los conceptos básicos útiles, se encuentran algunos teoremas
espaciales que dada la condición de perpendicularidad que siempre
van a cumplir las proyecciones, nos resultarán de suma utilidad. El
siguiente vídeo nos lo explica y además podemos ver su aplicación
directa:
Piziadas, también nos arroja luz sobre los conceptos básicos y
añade lo siguiente con respecto al plano formado por las
proyecciones de un punto:
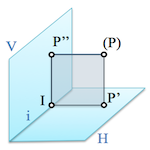 "La recta intersección de los dos planos, i, es la dirección común a ambos planos. Los tres planos se cortarán en un punto I.
"La recta intersección de los dos planos, i, es la dirección común a ambos planos. Los tres planos se cortarán en un punto I.Si proyectamos ortogonalmente el punto (P) sobre los planos H y V, las rectas (P)-P’ y (P)-P” serán ortogonales a ellos respectivamente.
El plano que contenga a (P)-P’ será ortogonal al plano H y de forma análoga, el plano que contenga a la recta (P)-P” lo será a V. Por lo tanto, si consideramos el plano formado por los puntos (P)–P’–P” y el punto I, este será perpendicular a V y H y por lo tanto a su dirección común, recta i.
Esta última propiedad nos permitirá establecer la relación perspectiva que existe entre dos proyecciones vinculadas."
Para
cerrar esta pequeña introducción al sistema diédrico, voy a lanzar
algunas conclusiones sobre el uso de ambos métodos.
- Ambos
métodos resultan de utilidad. Pero desde mi punto de vista, utilizar
la línea de tierra permite una asimilación global de su aplicación
mucho más directa y sencilla de entender. Además, si utilizamos diferentes fuentes de información, el uso de la línea de tierra dispone de materiales didácticos mucho más variados.
- Pese
a ser un método que juega con los mismos conceptos, el diédrico con
LT tiene el aspecto negativo de permitir una mecanización de
los mismos que en el diédrico directo no es posible. La mecanización del sistema libre, requeriría de más conceptos asimilados de los que requiere el uso de la LT.
- El sistema libre, necesita de una base sólida de geometría descriptiva, cuyo aprendizaje, también se haya basado en el razonamiento de los conceptos. Este aspecto, según se enfoque, puede ser positivo o negativo si tenemos en cuenta el estado actual de la enseñanza del dibujo.
Más
adelante, cuando el tiempo permita una puesta en materia más
focalizada, hablaremos de otras simplificaciones del diédrico
directo en comparación con el diédrico con LT.
¡Saludos
y ánimo a las compis y los compis del máster en la recta final!
______________________________________________________
Fuentes:
Piziadas
gráficas. http://piziadas.com/
Dibujo
técnico 1: Jesús Álvarez, José Luis Casado, María Dolores
Gómez. Editorial SM.
Geometría
descriptiva: Ricardo Bartolomé Ramírez
Canal Profesor de Dibujo (PDD). http://goo.gl/4lWWoY
Canal 8 cifras. https://goo.gl/wBZEv1




