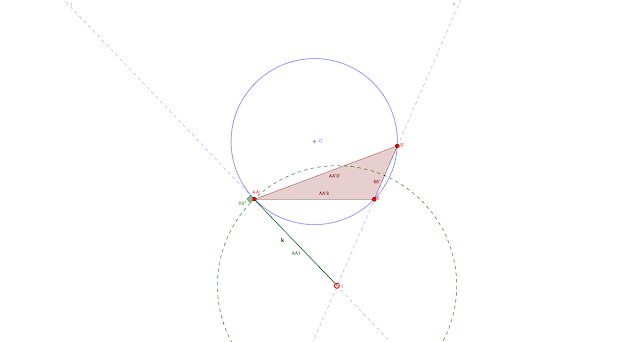
Dado un triángulo ABB', invertir la figura sabiendo que A es un punto inverso de sí mismo, es decir: A=A'
Como adivinaréis, el punto de partida de este problema, se encuentra relación que guardan las dos parejas de puntos proporcionadas con respecto al centro de inversión y por tanto de la circunferencia de autoinversión o circunferencia de puntos dobles (c.p.d). El concepto de potencia nos ayuda a saber que las dos parejas de puntos invertidos BB' y AA' son puntos concíclicos, es decir, que se encuentran en la misma circunferencia y que guardan una relación constante con el centro de inversión. En otras palabras, cada punto y sus inversos además de encontrarse en la misma circunferencia, están alineados con el centro de inversión.
Por tanto, una aproximación certera a la solución, será deducir que el centro de inversión se encuentra en la recta que pasa por BB'.
Hallar el centro de la circunferencia de puntos dobles requiere que ampliemos nuestros conocimientos de inversión un poco más:
- La circunferencia que contiene pares de puntos inversos, es inversa de sí misma si la potencia es positiva, es decir, si los puntos inversos se encuentran al mismo lado con respecto al centro de inversión.
- Esta circunferencia inversa de sí misma corta ortogonalmente a la circunferencia de autoinversión, por tanto contiene elementos dobles.
- Cuando la potencia es negativa, no se cumple la ortogonalidad con respecto a la circunferencia de puntos dobles (porque no podemos trazar tangentes desde el centro de inversiópn a la circunferencia inversa de sí misma), es decir: si la potencia es negativa, la circunferencia inversa de sí misma no contiene puntos (o elementos) dobles.
Lo entenderemos mejor si continuamos con nuestro problema.
Al darnos el triángulo como figura para invertir y conocer que A=A', no erraremos al afirmar que la potencia con respecto al centro de inversión (que estamos intentando hallar) es positiva. Es más, sabremos también que la circunferencia que contiene a ambas parejas de puntos inversos es inversa de sí misma al contener un elemento doble y por tanto ortogonal a la circunferencia de puntos dobles (c.p.d). La tangente que pasa por el punto AA' con respecto a la circunferencia que lo contiene nos da el centro de inversión y además la potencia (k).
Ya tenemos todo lo necesario para invertir la figura. Vamos por partes.
Invertir el segmento BB' será lo más sencillo, pues sabemos que al estar alineado con el centro de inversión, cada punto tiene a su inverso en la propia recta, por tanto:
El inverso de BB' es BB'.
Para invertir AA'B y AA'B' vamos a añadir otra característica de la inversión en el plano a nuestra lista:
- Al invertir una recta que no pasa por el centro de inversión lo que obtenemos es una circunferencia que sí pasa por el centro de inversión y viceversa (recordemos que la inversión es una transformación involutiva).
Sabiendo esto, simplemente tenemos que hallar los centros de las circunferencias que pasen por: AA', B' e I y AA', B e I. Los arcos de cirfunferencia que unan los puntos completarán nuestra solución.
Por último, añadiremos unos conceptos a nuestra lista.
La inversión en el plano:
Transformación homográfica.Tranformación con centro.Circunferencia de autoinversión o circunferencia de puntos dobles (c.p.d).Potencia de inversión positiva.
Relación constante (K) con respecto al centro de inversión.Dos puntos y sus inversos: conclíclicos.- Potencia negativa: la circunferencia inversa de sí misma no contiene puntos (o elementos) dobles.
- Circunferencia inversa de sí misma: corta ortogonalmente a la c.p.d.
- La inversión de una recta que no pasa por el centro de inversión es una circunferencia que sí pasa por el centro de inversión(y viceversa).
¡Hasta la próxima!
Fuentes:
Jose Luis Tabara Carbajo (canal de Youtube)